What is energy, actually?

The most famous asterisk in theoretical physics.

Think you know what energy is? You probably don’t. That’s okay. Einstein probably didn’t either, at least not in the context of his own masterpiece, general relativity.

Forget the pop-sci soundbites you hear from people like NDT. Energy is not simply “mass in motion” or “mass because (E=mc²)” or “the capacity to change” or even the neatly “conserved currency of our universe.” These definitions (to the degree they’re definitions) don’t hold up in dynamically curved spacetime.

Most likely, your GR instructor glossed over energy, perhaps mumbled something about “pseudo-tensors” under their breath, then quickly changed the subject. Why the rush? Why the evasion on such a supposedly fundamental concept? Physics professors skip energy like dads skip the sex talk—awkward mumbling and hope you never ask again.

The full, honest treatment is extremely messy, deeply controversial, and fundamentally unresolved even after a century. Einstein himself wrestled with it, and the compromises he made are still debated today.

Let’s talk about that mess.

Energy Conservation in (Dynamically) Curved Spacetime

The heart of the problem is that general relativity has two foundational pillars:

1. general covariance (physics laws don’t depend on coordinates)

2. the equivalence principle (gravity = local acceleration)

In flat spacetime, energy-momentum conservation is quite neat: ∂ᵤ Tᵘᵛ = 0, where Tᵘᵛ is the stress-energy tensor of matter. GR looks similar: ∇ᵤ Tᵘᵛ = 0. But that upside triangle ∇ᵤ is the covariant derivative, which requires extra machinery (something called a connection) to employ.

Curt’s aside: Apologies for these ASCII symbols, which look horrible compared to in-line LaTeX. Hopefully, Substack will soon add native in-line LaTeX rendering.

In coordinates, expanding it out, you get extra terms: ∂ᵤ Tᵘᵛ + Γᵘᵤα Tᵃᵛ + Γᵛᵤα Tᵘᵃ = 0. Energy seems to leak into or out of the gravitational field itself.

Einstein, wanting something conserved, cooked up a fix (he did that with the cosmological constant as well). Physics is largely a game of whack-a-mole whereby fixing one problem adds another.

Anyhow, Einstein added a term tᵘᵛ. This is the infamous “pseudo-tensor” meant to represent the energy of the gravitational field itself. This combination, Ẽᵘᵛ = Tᵘᵛ + tᵘᵛ, actually does satisfy a simple conservation law:

\(\partial_\mu (\sqrt{-g} \tilde{T}^{\mu\nu}) = 0\)

Seems fine, however if you examine it, you realize the price was deceptively steep: tᵘᵛ is not a tensor.

That means it depends entirely on your chosen coordinates! Not cool bro.

In GR, non-tensorial quantities are usually considered mathematical artifacts, not physical realities. This is made blatant when you learn the bundle differential geometric view. Anyhow, this breaks the whole spirit of general covariance.

The Pseudo-Tensor Dilemma

Saying “tᵘᵛ is gravity’s energy, and gravity vanishes locally via the equivalence principle, so its energy should be coordinate-dependent” sounds suspiciously like post-hoc justification for a kludge. Is it? And is there a better way?

Well, if your spacetime has symmetries, then yes. If there’s a time-like Killing field ξᵥ (meaning spacetime looks the same along the “flow” of ξ), then you can define a genuinely conserved, coordinate-independent energy: E = ∫Σ [d³x]ᵤ √-g Tᵘᵥ ξᵥ.

Curt’s aside: This isn’t a murderous field. It’s named after Wilhelm. There is a concept of Thanos-like annihilation in possibility space, though, called Gotterdammerung events.

Why is this conserved? Because ∇ᵤ(Tᵘᵥξᵥ) = (∇ᵤ Tᵘᵥ)ξᵥ + Tᵘᵥ(∇ᵤ ξᵥ). The first term is zero (from ∇ᵤ Tᵘᵥ = 0), and the second vanishes because Tᵘᵥ is symmetric and the Killing equation is:

\(\nabla_\mu \xi_\nu + \nabla_\nu \xi_\mu = 0\)

The problem is that most spacetimes, especially realistic cosmological ones, don’t have exact Killing vectors.

So this definition, while clean, is limited.

Energy in GR is like my friend's veganism… loudly declared, but suspiciously flexible.

Misconceptions About Vacuum Solutions

Consider the Schwarzschild black hole. Textbooks often call it a “vacuum solution” (Tᵘᵥ = 0 everywhere). If that were true, E would be zero. A “vacuum solution” is a misnomer because the Schwarzschild solution isn’t truly vacuum. It has a delta-function singularity in Tᵘᵥ exactly at r = 0, representing the collapsed matter source:

\(T^0_0 \propto M \delta(r)/r^2\)

Curt’s aside: Yes, it should be noted that mathematically, Tᵘᵥ = 0 for r > 0 and r = 0 is a curvature singularity, the parameter M comes from this source...

Using the time-like Killing vector ξᵥ = -δᵥ₀ (which is Killing outside the horizon), E = ∫ d³x √-g T⁰ᵥ ξᵥ correctly gives M, the black hole mass (after properly handling the singularity). The “vacuum” story is a convenient lie that hides the source, likely contributing to why this covariant definition wasn’t embraced sooner.

Energy in Neutron Stars and Beyond

What about something less singular, like a neutron star? For a static, spherical star, E involves integrating the density ρ(r) times √-g₀₀ gᵣᵣ. Compare this to the standard ADM energy (often called Misner-Sharp mass in this context, and defined via integrals at spatial infinity, assuming spacetime suitably flattens far from the source), which just integrates ρ(r) without the √-g factor. They aren’t the same.

In the Newtonian limit (weak gravity), Eₐ looks like the total rest mass plus the gravitational binding energy (a negative term). E, however, looks like the rest mass energy *evaluated in the background potential. The issue is that BOTH seem reasonable, yet they differ—E is covariant, Eₐ isn’t (it relies on asymptotic flatness).

Okay, so which one is “the” energy? Depends on what question you’re asking, perhaps? But then does that mean “energy” depends on what you ask? Also, not cool.

Furthermore, what if there’s no Killing vector? No perfect symmetry?

We saw E = ∫ √-g Tᵘᵥ ξᵥ [d³x]ᵤ was conserved if ∇ᵤ ξᵥ + ∇ᵥ ξᵤ = 0. It turns out, a quantity S = ∫ √-g Tᵘᵥ ζᵥ [d³x]ᵤ is still conserved if a more general condition holds: Tᵘᵥ ∇ᵤ ζᵥ = 0, for some vector field ζᵥ. This ζᵥ doesn’t need to be a Killing vector.

Can we always find such a ζᵥ? And what does this S mean?

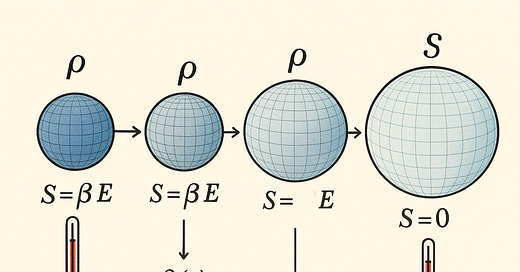
Energy and Entropy in Cosmology

Let’s look at the expanding universe (FLRW metric).

There’s no time-like Killing vector. The standard energy E = ∫ d³x \, a³ ρ (where ‘a’ is the scale factor) is famously not conserved. As the universe expands, energy gets diluted oddly (Ẽ = -3 (ȧ/a) P V ≠ 0).

However, you can find a ζᵥ = β(t) ξᵥ₀ (where ξᵥ₀ = -δᵥ₀ is just the standard time direction and β is a time-dependent function) that does satisfy Tᵘᵥ ∇ᵤ ζᵥ = 0. The condition forces ẏ/β = 3(P/ρ)(ȧ/a). The conserved quantity S = ∫ √-g Tᵘᵥ ζᵥ [d³x]ᵤ = β E then turns out to obey:

\(dS/dt = \beta(dE/dt + P dV/dt)\)

If that looks familiar to you, it’s because you’re right. It is indeed awfully close to the First Law of Thermodynamics, TdS = dE + PdV, provided you interpret S as total entropy and β as 1/T (inverse temperature)!

So, in cosmology, perhaps the conserved “thing” isn’t energy, but entropy, and β(t) tells us how the universe cools as it expands?

Gravitational Waves and Energy

This brings us back to gravitational waves. LIGO detects them (something previously thought impossible because of how weak gravity waves are), and binary pulsars spin down exactly as predicted if they’re losing energy to gravitational waves... surely gravitational waves carry energy?

Well, yes, in effective field theory approximations or using pseudo-tensors (such as the Isaacson effective stress-energy tensor derived from averaging metric perturbations), they do. But try to use a fully covariant, Tᵘᵥ-based definition like E or S.

Pure gravitational waves are vacuum solutions (Tᵘᵥ = 0), so these definitions give... zero energy.

Curt’s aside: There are other covariant quantities like the Bel-Robinson tensor, which are non-zero for gravitational waves, but their physical interpretation as a definitive energy-momentum measure is debated, and the point about their not being a unique characterization of energy still stands.

Does this mean gravitational waves don’t carry energy fundamentally within GR? Or does it mean our covariant definitions based solely on Tᵘᵥ are “incomplete”? Perhaps we do need a way to account for “gravitational energy,” but the pseudo-tensor isn’t it, unfortunately.

The Ongoing Quest for Energy Definition

So where does this leave us? Defining energy in GR isn’t trivial.

Well, technically, defining what light is isn’t trivial either!

Pseudo-tensors give conservation but break covariance. Covariant definitions linked to Tᵘᵥ work cleanly with symmetries but fail for general spacetimes or pure gravity. Generalizations like the entropy-like S hint at deeper structures but lack universal interpretation.

Perhaps the seemingly indubitable structure of Einstein’s equation—matter Tᵘᵥ sources curvature, but curvature doesn’t directly source itself in the same manner—implies only “matter energy” is truly well-defined…

…Or maybe, after 100+ years, we still just haven’t figured it out. The search continues.

---

This analysis heavily inspired by the 2022 work of Sinya Aoki. Refer to that arXiv pre-print for more detail.

I want to hear from you in the Substack comment section below. I read each and every response.

—Curt Jaimungal

PS: Please do consider becoming a paying member on this Substack. This is how I earn a living, as I’m directly reader-supported. Moreover, you’ll get a slew of exclusive content. If you like the “free” content, you’ll love the members-only content. Anyhow, thank you dearly either way.